An incomplete guide to E2E encrypted communication for groups

One of the largest remaining challenges in secure communication is group communication. Signal brought on a wave of awareness towards end-to-end encrypted messaging. The problem is simple in the two-party setting: two individuals send messages back and forth, and the messages should only be available on their devices and nowhere else. Any party eavesdropping on the communication channel should not be able to read any messages, nor should the messaging platform.

The Signal protocol has solved almost all exciting problems in the two-party setting: military-grade resilience, break-in recovery, and forward security. Every message is encrypted with its own unique message key. If your keys are compromised at some point, it does not allow the attacker to read past messages or keep reading messages far into the future. Signal also has group chats. However, each group has a size limit of 1000 members. Group voice or video calls have a 40-member limit.

This blog post will discuss Signal's end-to-end (E2E) encrypted group chat protocol and a few other notable open-source protocols: Matrix's Megolm and XMPP's OMEMO. We skip discussing Telegram as it is only partially open-source. Billions of people use Signal's secure communication protocol as Whatsapp, Skype, and Messenger have all adopted it. Before we get into it, it is essential to discuss what all E2E encrypted group chats look like today. Most of them look like some version of the following:

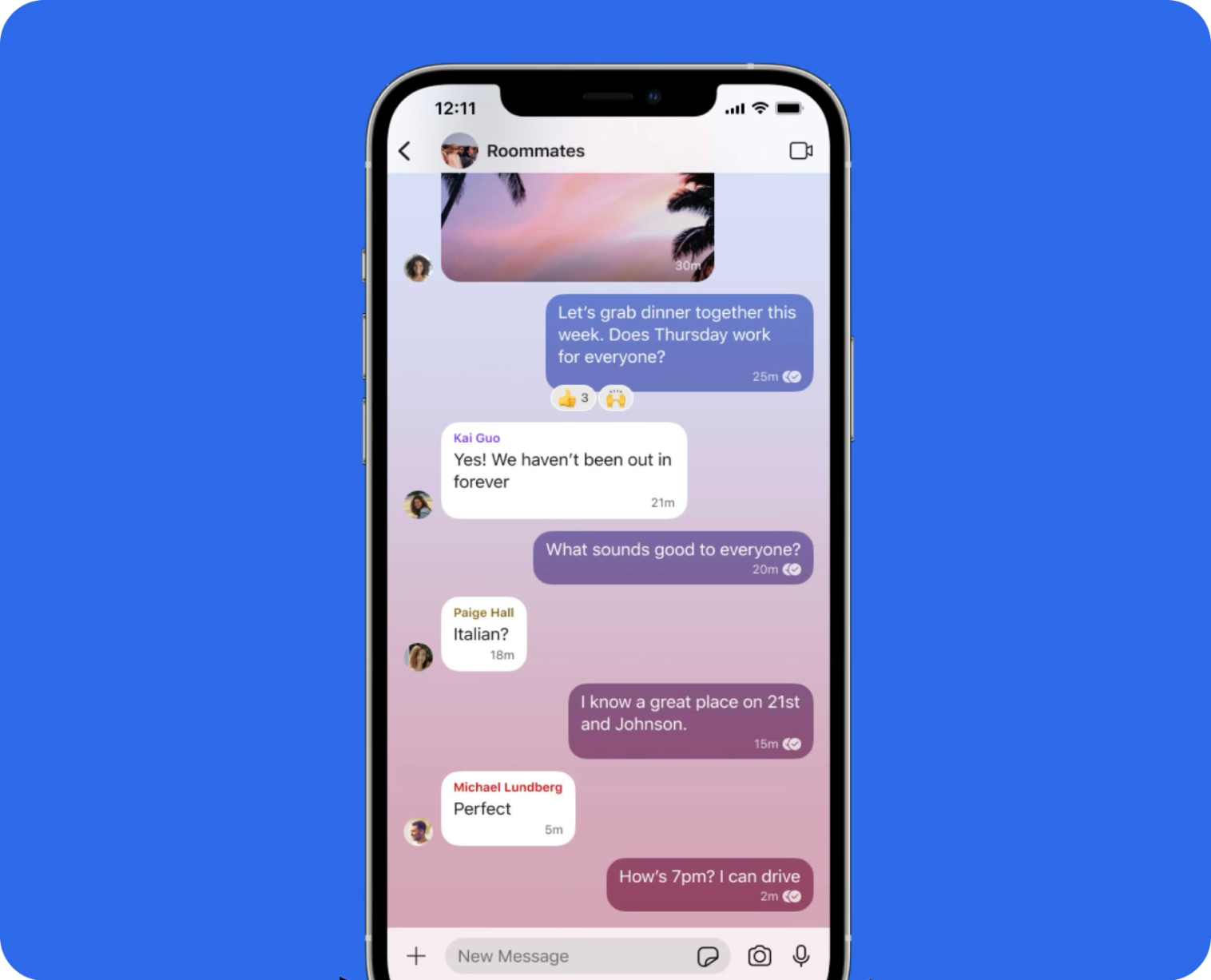
These are clearly meant for very small groups. As group sizes grow, the experience declines in multiple ways. Firstly, opening an active group chat after a few weeks is a nightmare we have all been through. There is no good way to extract relevant information, and searching for keywords can be wildly inefficient and slow. From a protocol support standpoint, many challenges arise with the increase in traffic. The number of communication increases, latency issues become more challenging, and message ordering becomes painful. To Signal's credit, they deal with these challenges quite well in smaller groups. But the problem is the form factor of these groups, in the 10-1000 member group size range.

Reddit's interface is much easier to work with in these group sizes. Filters and flairs make it easier to sort through stuff, threading makes sub-conversations easy to follow, and upvotes make it easier to manage reputations. Notably, Reddit also access-gates certain communities. You can become a part of these "private" subreddits if approved by the community moderators. Beyond that, there is no extra layer of security or privacy securing communications in a private subreddit from Reddit as a platform. Other platforms that allow access-gated communities with conversation threading also follow similar policies. However, even if suddenly Reddit decided to develop an E2E encrypted secure communication protocol for private subreddits, the messages are only as private as your trust in the group. Such a protocol can be very interesting with watermarking-type properties for detecting traitors. Let's leave this pandora's box for the future.

Signal Protocol

We will now go over the Signal protocol in some detail. Megolm and OMEMO would be easier to describe and understand post this. Signal chooses the most demanding and most respectable path to achieve the goal of establishing E2E encrypted group chats. In this protocol, group conversations are treated just like two-party communication. Therefore, the Signal protocol establishes an encrypted communication channel between all unique sets of two parties within a group. This might sound like a crazy, inefficient idea, but it actually does not change much: think of the unencrypted setting. The server still sends out a message per group member in the unencrypted setting. The only cost incurred in this encrypted version is on the sender side: the sender encrypts the messages once for every group member other than themselves.

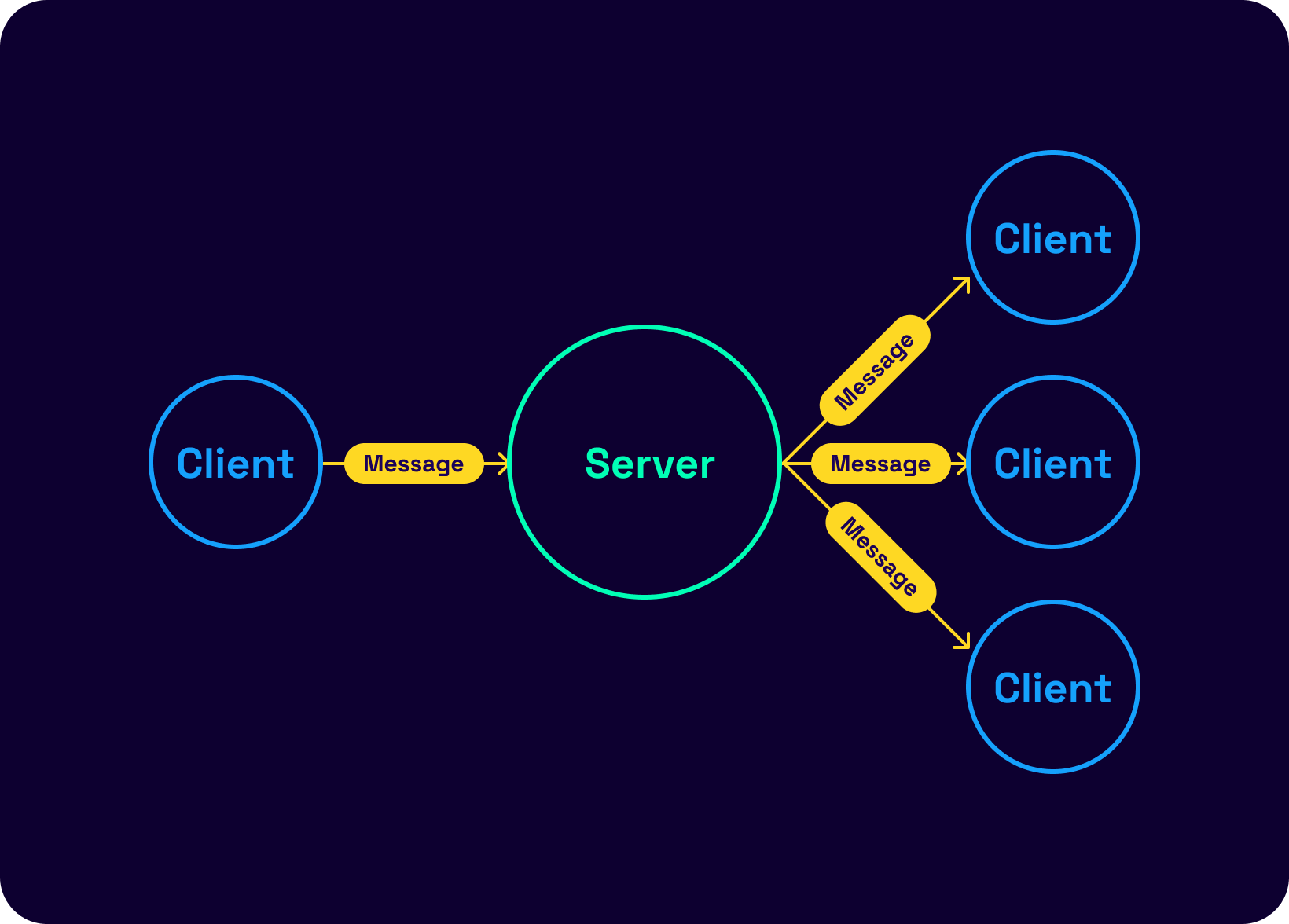
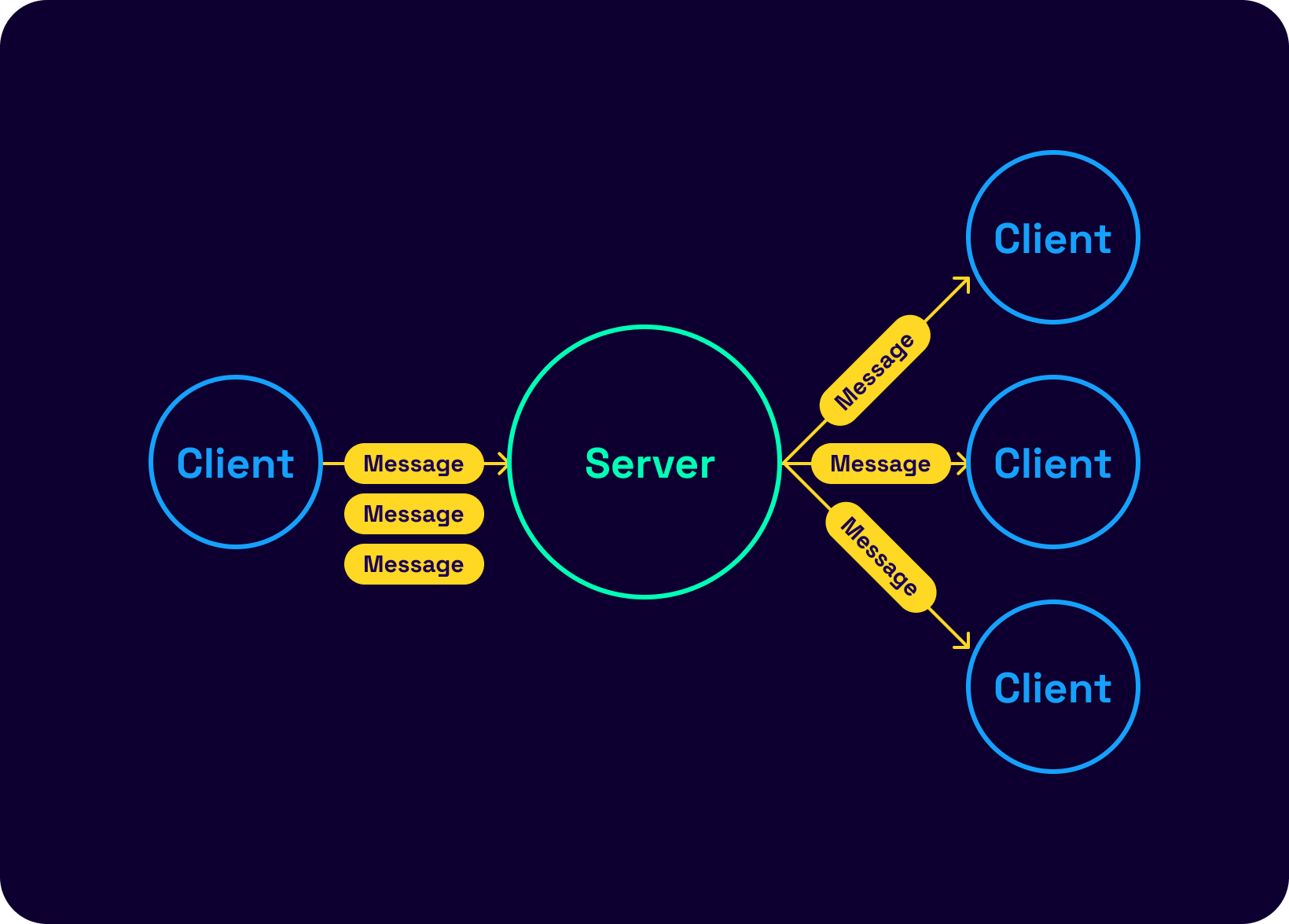
Thankfully, an optimization allows sending the message payload once while attaching a signing key pair per group member. Something resembling the following:

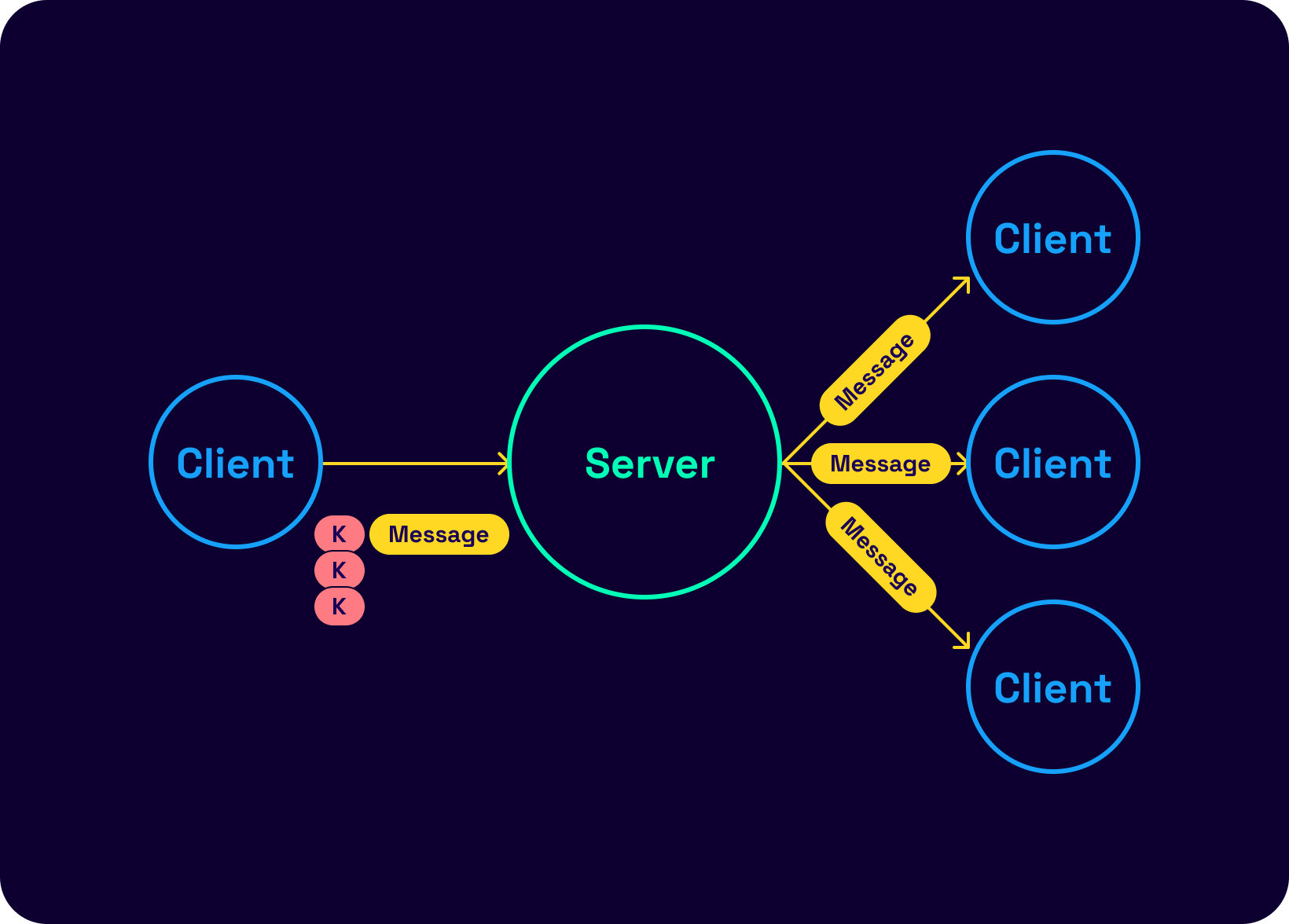
Before we can talk about optimization, the following crucial pillar of the Signal protocol must be understood.

Double Ratcheting

The Signal protocol encrypts every message with its unique key, which is excellent for its security. The double ratcheting algorithm deals with the crucial component of cryptographic key derivation and exchange. The name "double ratchet" refers to the mechanism used in the algorithm to update the encryption key for each message. The ratchet works by incrementally updating the encryption key with each message, ensuring that the encryption key for each message is unique and cannot be used to decrypt any previous or future messages. This mechanism is called a "ratchet" because it allows for the key to advance or "ratchet forward" in a secure and controlled manner. The rest of this section is for an audience with a more technical background. Please feel free to skip to the next section if needed. Double ratcheting is also used in the other protocols; hence, it is essential to spend some time understanding.

There are two cryptographic key derivations and exchanges that happen in one single step of this algorithm. The name "double ratchet" in the context of Signal's encryption protocol refers to combining two key update mechanisms: the symmetric key ratchet and the Diffie-Hellman ratchet. The symmetric key ratchet updates the encryption key for each message, ensuring that each message has a unique encryption key. Symmetric/Private-key cryptography is generally used to encrypt messages in high-frequency communication due to blazing-fast performance and hardware optimizations. The tradeoff is that the security of this kind of cryptography is not based on algorithms that have been extensively analyzed and tested, and no efficient method for breaking them has been found. This is unlike public key cryptography, which relies on the mathematical difficulty of certain problems, such as the RSA problem or the discrete logarithm problem.

Attached below is a flow chart of how this key derivation process works. The key derivation function takes as input a chain key and a constant and outputs the next chain key and a message key (used to encrypt the next message).

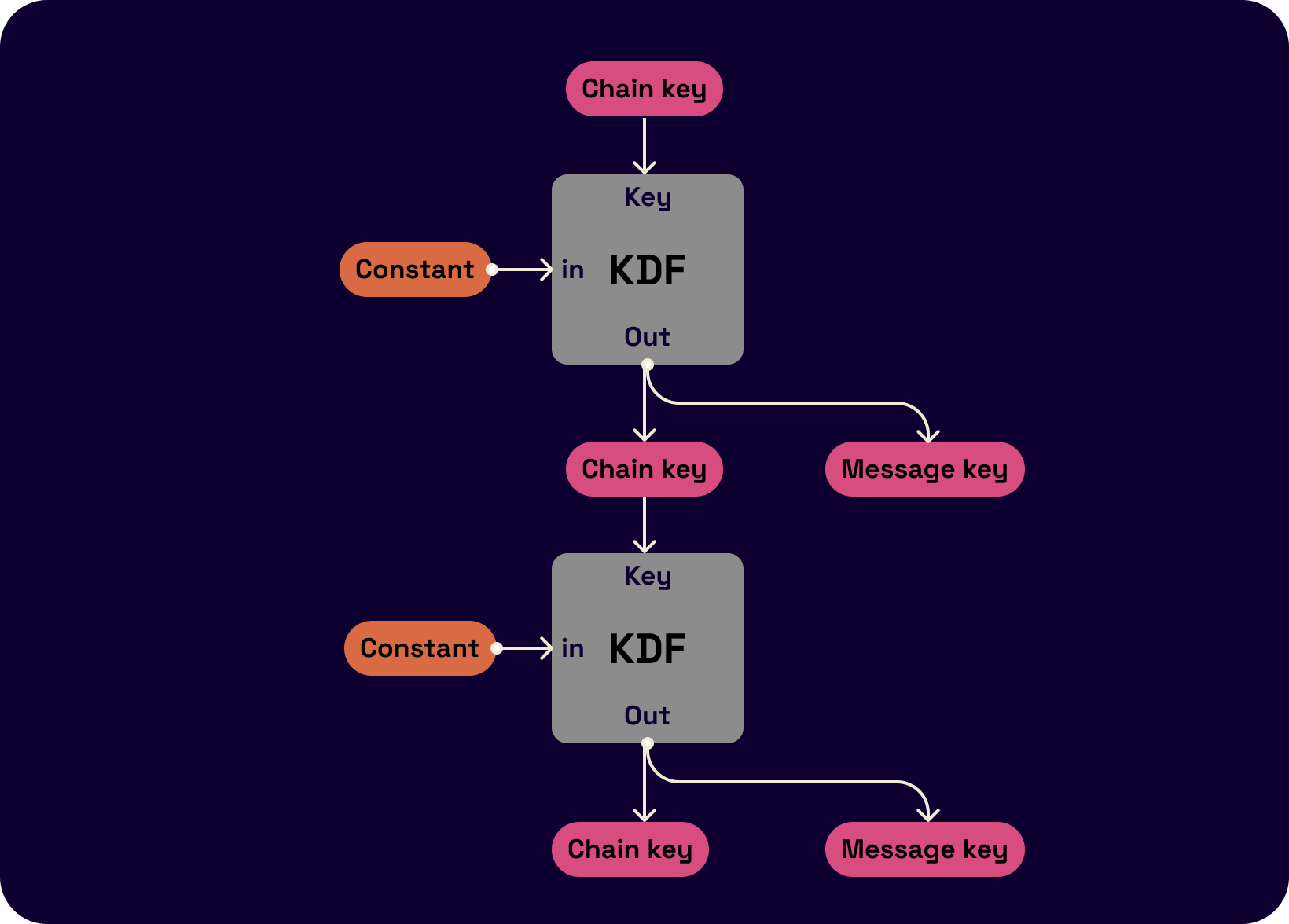
In the two-party setting, there are two KDF chains. Let's say the parties are Alice and Bob. One of the chains is Alice's sending chain (and Bob's receiving chain,) and the other is Bob's sending chain (and Alice's receiving chain). The goal is that for each sent and received message, Alice and Bob should be able to derive the message key. Each of these two chains needs key updates every time a message is sent. To update keys, a symmetric-key ratchet is used. One symmetric key ratchet step consists of calculating the next chain key (used to continue the chain) and message key (used to encrypt the current message) from a given chain key. Once the parties have the same message key, they can encrypt and send (if it's an outgoing message) and know that the other party can decrypt the ciphertext and vice-versa.

However, if some attacker steals one party's sending and receiving chain keys, the attacker can compute all future message keys and decrypt all future messages. A Diffie-Hellman ratchet is used to prevent this issue: the parties take turns replacing what is input to the KDF. This works because if one of the party's keys is compromised, while the attacker knows the current ratchet key, it is soon replaced by an uncompromised key from the other party.

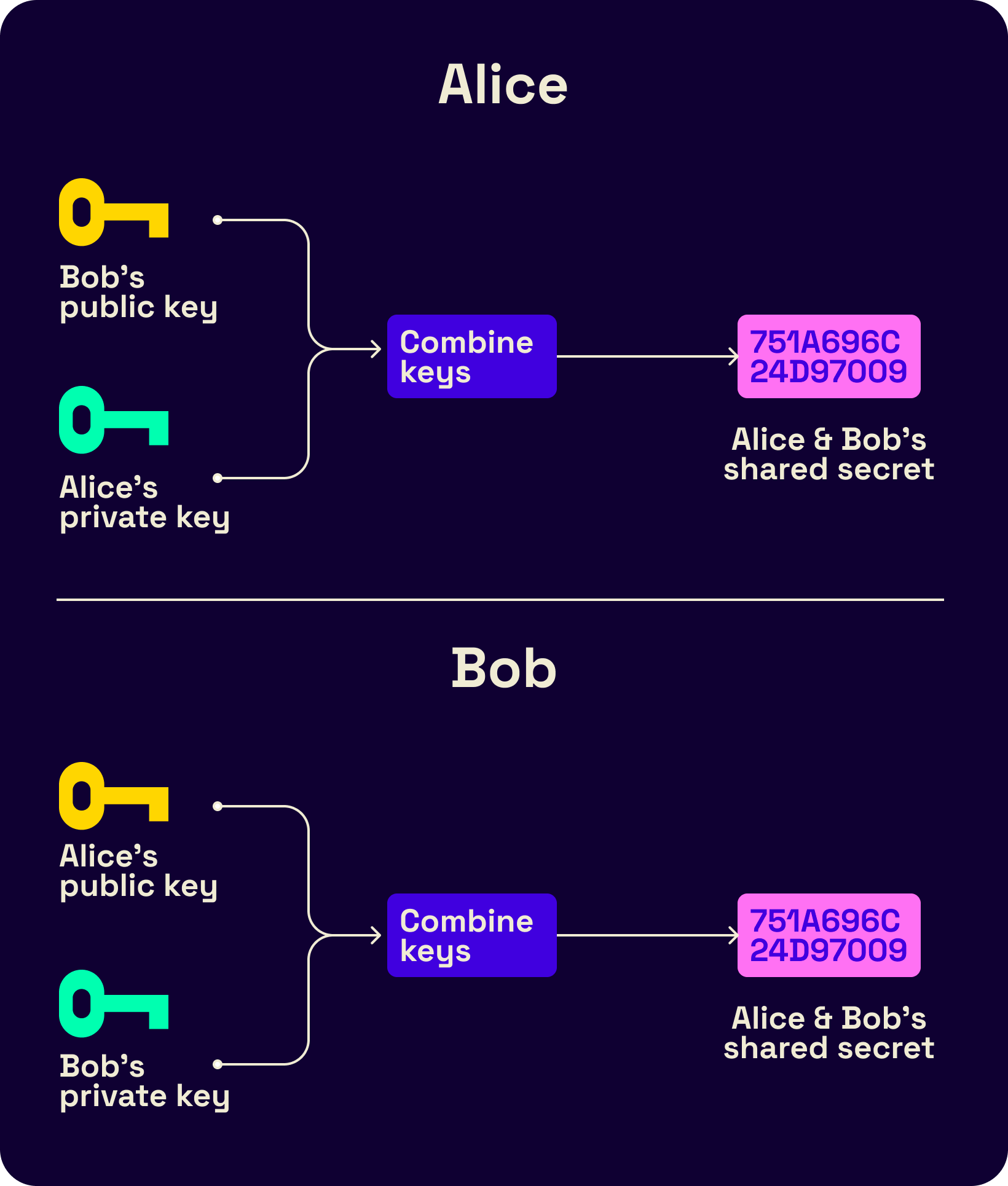
The Diffie-Hellman (DH) ratchet allows for the secure exchange of encryption keys between two parties, ensuring that the encryption keys are updated in a secure and forward-secret manner. This simply means that the party who selects the next KDF input securely shares them with the other party using the DH ratchet. Together, these two ratchets provide strong security guarantees for encrypting messages in the Signal protocol. The use of two ratchets helps to prevent a potential attacker from being able to decrypt the messages by intercepting the key updates.

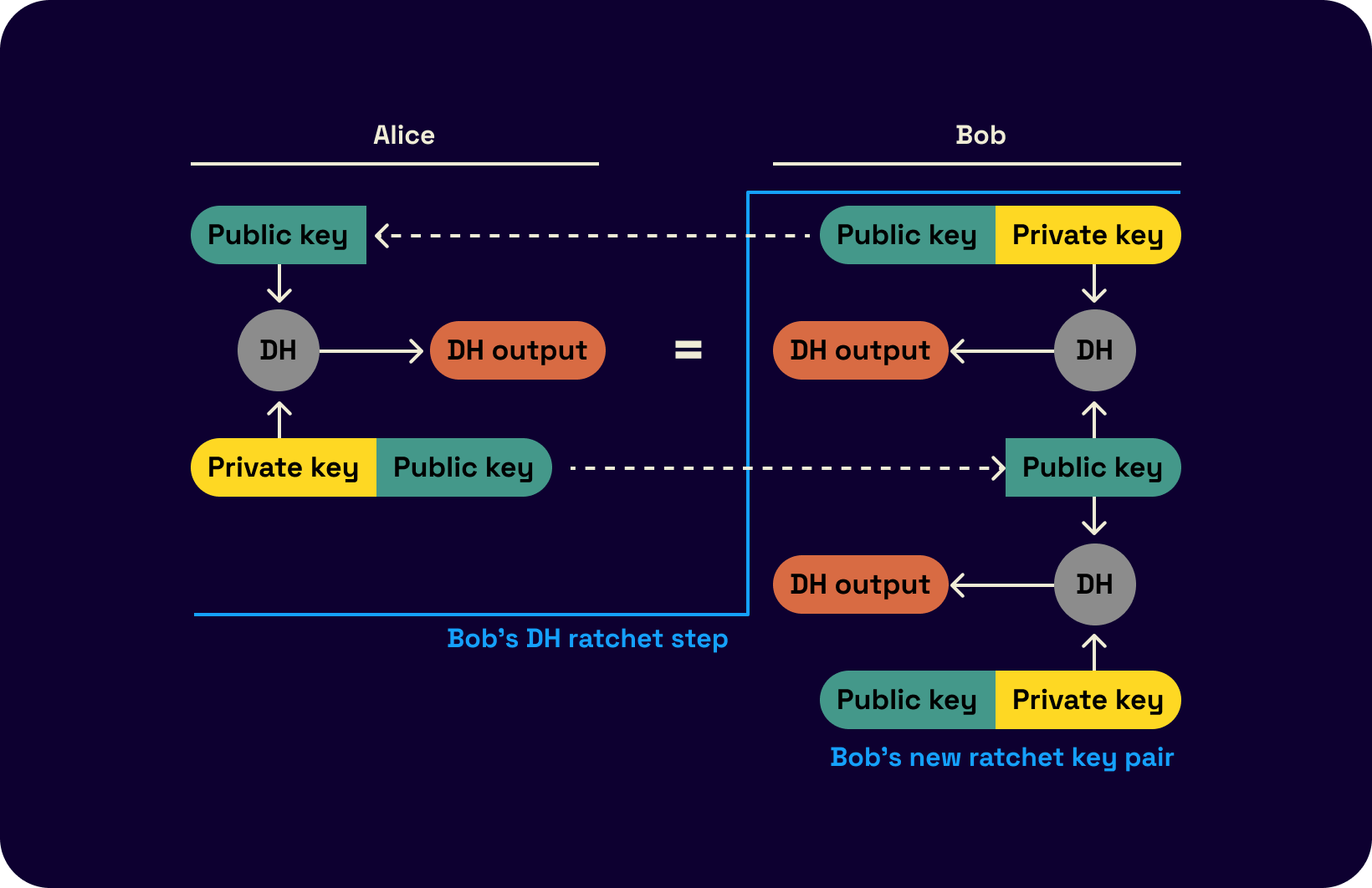
The following visual flowcharts of the process from Trevor and Moxie's original double ratchet spec demonstrate an example run of the protocol. The DH ratchet output is one of the inputs to the KDF as follows.

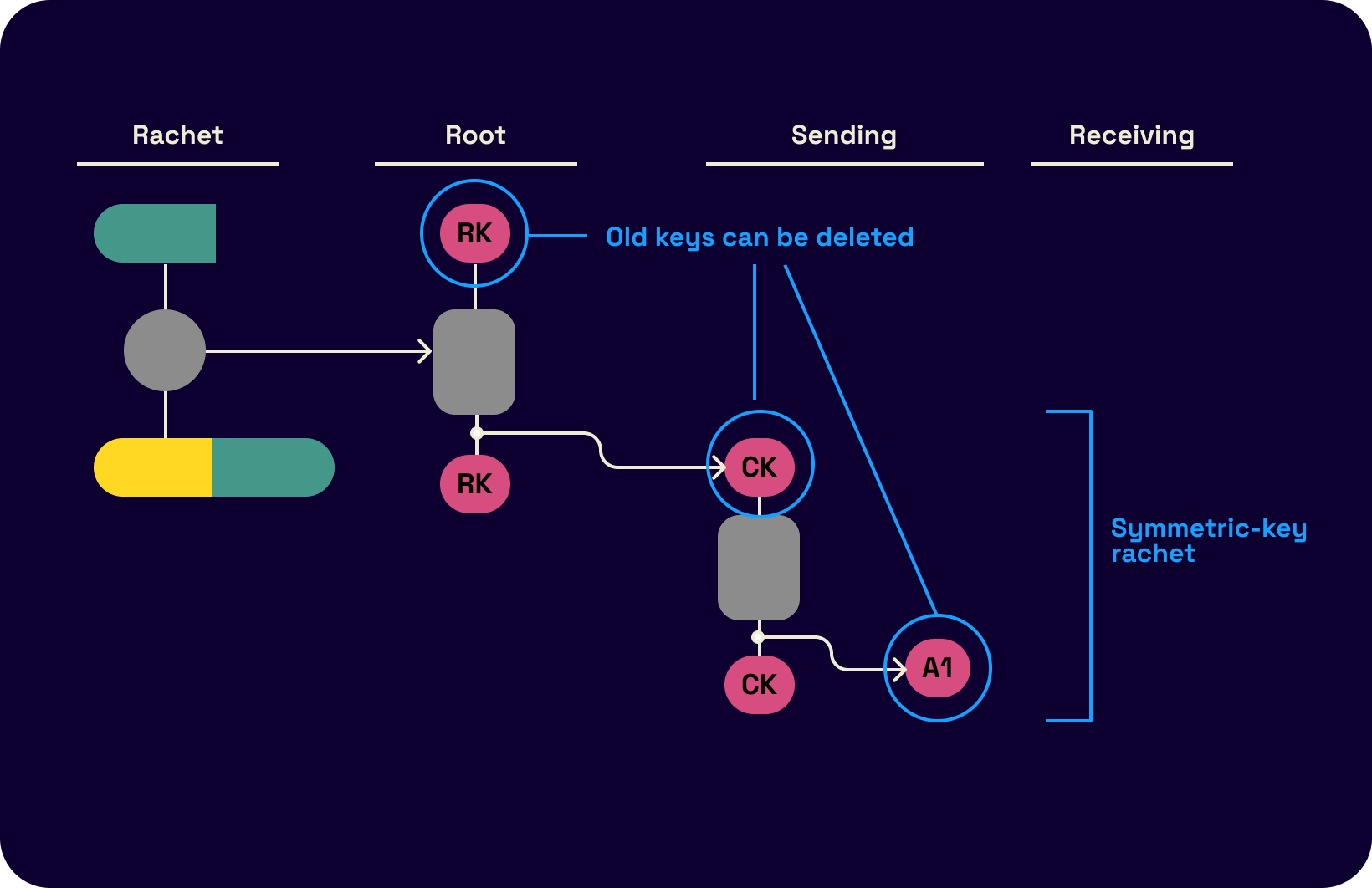
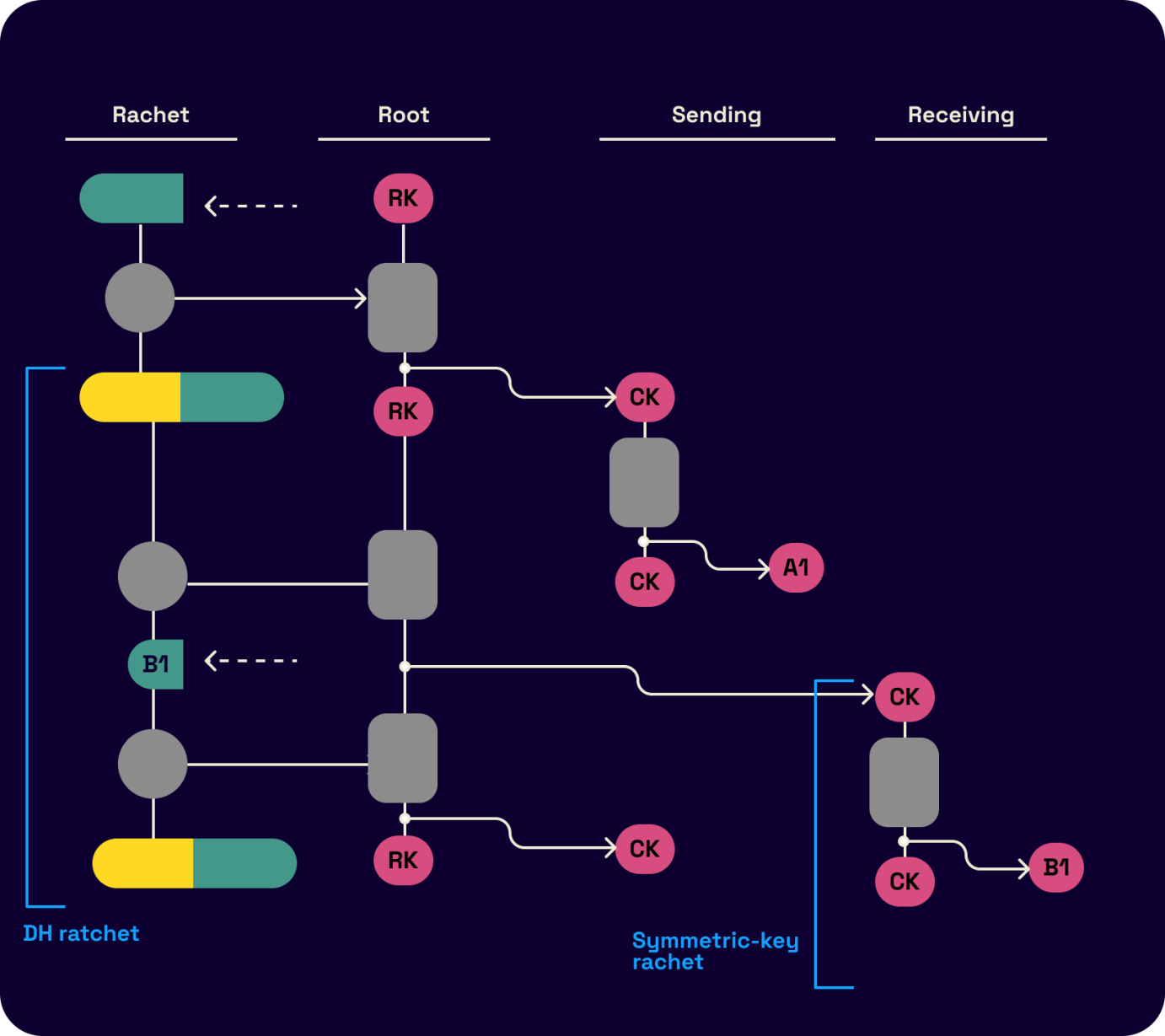
Message headers include the message's order sequence in the sending chain to allow the discarding of out-of-order messages. Missing details here, including the header encryption variant of the protocol, can be extracted from Signal's protocol documentation.

Matrix's Megolm Protocol

Megolm is an AES-based cryptographic ratchet intended for group communications that was designed with the following goal:

The Megolm ratchet is intended for encrypted messaging applications where there may be a large number of recipients of each message, thus precluding the use of peer-to-peer encryption systems such as Olm.

Without diving much deeper into the technical details, each Megolm ratchet has 4 rounds that are outputs of a hash function. Each participant in a group conversation has their own Megolm session that consists of the following three parts:

• a 32 bit counter, \(i\)
• an Ed25519 keypair, \(K\)
• a ratchet, \(R_i\)​, which consists of four 256-bit values,
  \(R_{i, j}​\) for \(j \in 0,1,2,3 \)

Other participants in the conversation can decrypt messages once they have the session data. Session data is shared using a secure peer-to-peer channel. The session data is authenticated using a signature scheme, and then each participant can store their copy of this session's counter, ratchet, and public-key and update it when needed. Messages are encrypted using keys obtained by advancing the ratchet. Megolm uses AES-256 in CBC mode for encryption with PKCS#7 padding and HMAC-SHA-256 (truncated to 64 bits) for authentication.

The Megolm protocol, while simpler, has the following limitations:

• Message replays: An attacker can re-send copies of an older message, and the recipient cannot detect this replay. However, this is easily resolved by adding encrypted header sequence numbers to the messages.
• Lack of consistency: There is no guarantee that all recipients receive the same message. This protocol does not guarantee in-order message delivery.
• No backward security: Current messages are not secret if the protocol has been compromised in the past.
• Partial forward security: Current communication should remain secure when looking forward to a potential future compromise. This can be ensured in Megolm if applications do not use session keys indefinitely.
• Dependence on a direct channel for key exchange: Since there is a dependence on the direct, peer-to-peer channel to establish a session, if this channel is not secure, the entire session is compromised.

XMPP's OMEMO Protocol

This protocol was proposed to mitigate the usability drawbacks of E2E encryption schemes used in the XMPP ecosystem. Past versions of protocols like OTR messaging and OpenPGP allowed conversations between only two clients, while requiring both clients to be online for the conversation. OMEMO uses Signal's Double Ratchet protocol, which we discussed earlier. However, OMEMO makes one crucial improvement over Signal. OMEMO decentralizes the initial scheme used to set up user keys to start the protocol. Signal requires the central server to store pre-keys for every registered client. Personal Eventing Protocol (PEP) is an existing XMPP extension that allows clients to randomly generate and advertise their pre-keys to XMPP servers. Pre-keys are the keys used to start communication with other individuals. Besides this change, the difference between the OMEMO and the Signal protocol is not highly significant.

To conclude, a limited number of open-source protocols successfully achieve E2E encrypted group conversations. The Signal protocol's work in this area has served as a foundation for most other protocols. Now that this technology has been battle tested to a good degree, it is interesting to explore how it can provide a qualitatively different encrypted group chat alternative. Cryptographic tooling is making leaps every year. Computing on encrypted data is a crucial sub-area that will allow platforms to allow encrypted communication while still ensuring that the users are not engaging in illegal activities. Many exciting directions remain open for the future!